- George Biddel Airy, Esq., A.M, F.R.S., Astronomer Royal
- Originally Published 1830
- Encyclopædia Metropolitana, Volume V, Article: Figure of the Earth
- Pages 185-260
- Specific numbers on Page 240
- a = 20,923,700 feet = 6,377,543.76 meters
- b = 20,853,810 feet = 6,356,241.288 meters
- Direct PDF Download
- Alexander Ross Clarke
- Published 1833
- Account of the Observations and Calculations, of the Principal Triangulation; and of the Figure, Dimensions and Mean Specific Gravity of the Earth as Derived Therefrom
- Survey of Great Britain
- a = 20,927,005 feet = 6,378,551.12 meters
- c = 280.4 feet = 85.47 meters
- https://books.google.com/books?id=DKELAQAAIAAJ
- Direct PDF Download
- Friedrich Wilhelm Bessel
- Published 1841
- Astronomische Nachrichten 333 and 438
- a = 3,272,077.14 toises = 20,922,829.22 feet = 6,377,278.35 meters
- b = 3,261,139.33 toises = 20,852,888.96 feet = 6,355,960.55 meters
- Astronomische Nachrichten 333:
- Astronomische Nachrichten 438
- Sir George Everest
- Published 1847
- Account of the Measurement of Two Sections of the Meridional Arc of India between the Parallels of 18° 3′ and 29° 30′
- a = 20,920,902 feet = 6,376,690.93 meters
- b = 20,853,642 feet = 6,356,190.08 meters
- https://books.google.com/books/about/An_Account_of_the_Measurement_of_Two_Sec.html?id=ne82AQAAMAAJ
- Direct PDF Download
 “Transcontinental Triangulation and the American Arc of the Parallel”
“Transcontinental Triangulation and the American Arc of the Parallel”
- Published 1900
- Ocean to ocean survey. Shows triangulation with spherical excess.
- Page 221 for Spherical Excess
- From page 901 of the PDF, number 3 in the list is the primary result of this survey.
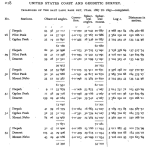
- a = 6,377,912 meters
- b = 6,356,309 meters
- https://geodesy.noaa.gov/library/pdfs/Special_Publication_No_4.pdf
- Direct PDF Download: Transcontinental Triangulation and the American Arc of the Parallel
- “The Figure of the Earth and Isostasy from Measurements in the United States”
- Published 1909
- Used the results from several surveys to determine the equatorial and polar radius of the earth.
- Page 174 has the conclusions of the computations.
- a = 6,378,283±34 meters
- b = 6,356,868 meters
- https://hdl.handle.net/2027/hvd.hnwwbh
- Direct PDF Download
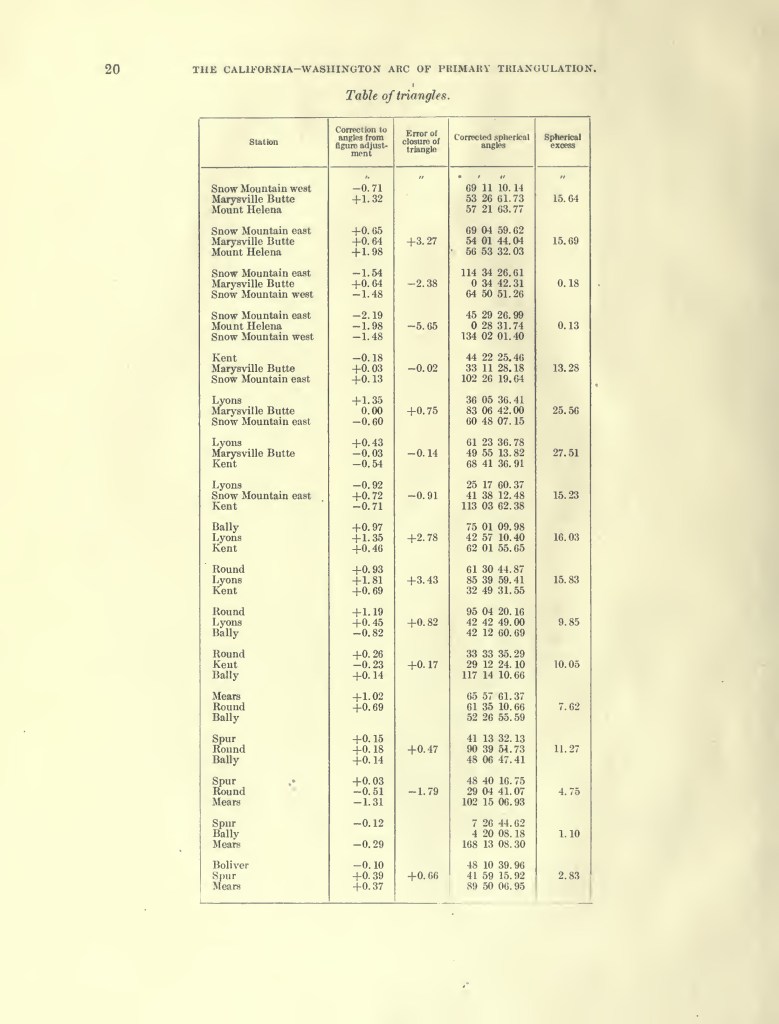
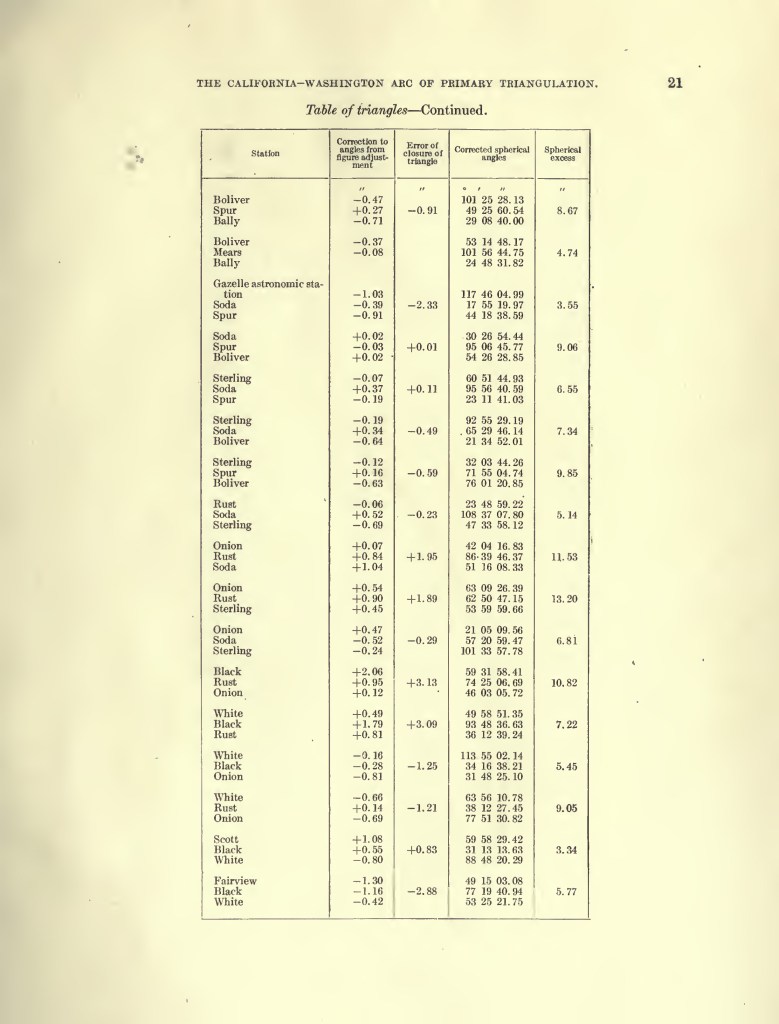
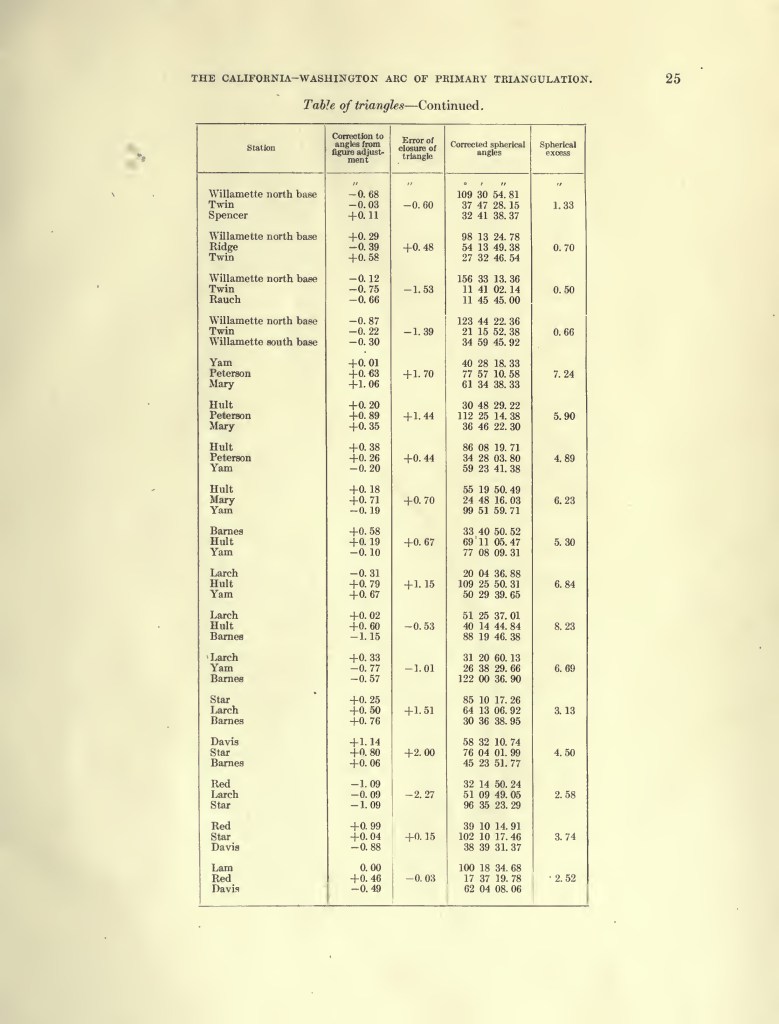
Spherical Excess
For a triangle on a plane, the sum of the interior angels is 180°. For a triangle on a sphere, the sum of the interior angles must be more than 180°. The amount over 180° is called “spherical excess”.
- “The California Washington Arc of Primary Triangulation 1913”
- See pages 22-31 of the PDF for examples of spherical excess.
- Direct PDF Download: The California Washington Arc of Primary Triangulation 1913
- “Geodesy primary triangulation on the 104th meridian and on the 39th parallel in Colorado Utah and Nevada”
- See page 62 for Spherical excess example.
- Direct PDF download: Primary Triangulation on the 104th Meridian and on the 39th Parallel in Colorado Utah and Nevada 1914







Overview of several different measurements circa 1906:
History of the Determination of the Figure of the Earth from Arc Measurements
Some measurements from this overview:
| Year | People | Page | Measurement | Location | Publication |
| 1729 | Snell, Cassini, Muschenbroek | 8-9 | 57,033 toises to the degree latitude = 69.07 miles 3,957.42 miles radius = 6,368.85 km radius | Netherlands | |
| 1633-1635 | Richard Norwood | 9-11 | 367,200 feet to the degree latitude = 69.55 miles 3,984.66 miles radius = 6,412.69 km radius | England | Link Direct Download |
| 1669 | Jean Picard | 13-16 | 57,060 toises to the degree latitude = 69.10 miles 3,959.29 miles radius = 6,371.86 km radius | France | Link Direct Download Page 197 of the publication |
| 1737-1738 | Maupertuis, Clairaut, Canus, Le Monnier | 20-28 | 57,437.9 toises to the degree latitude = 69.56 miles 3,985.51 miles radius = 6,414.06 km radius | Lapland | |
| 1737-1743 | Godin, Bougeur, De la Condamine | 28-33 | 56,746, 56,749, and 56,768 toises by different methods to the degree latitude 68.72-68.75 miles to the degree latitude 3937.5-3939.0 miles radius 6336.8-6339.25 km radius | Peru | |
| 1744 | Jaques Cassini, et al | 33-36 | 57,084, 57,071, 57,040, 57,048.5 toises by different baselines | France | |
| 1750-1751 | Marie, Boscovich | 36-41 | 56,979 toises to the degree latitude = 69.00 miles 3,953.67 miles radius = 6,362.81 km radius | Italy | |
| 1752 | Lacaille | 41-43 | 57,034.4 toises to the degree latitude = 69.07 miles 3,957.51 miles radius = 6,369.00 km radius | South Africa | |
| 1763 | Mason, Dixon | 46-55 | 56,888 toises to the degree latitude = 68.89 miles 3,947.36 miles radius = 6,352.65 km radius | North America | Link Direct download Page 326 of publication |
Note: the first measurement of the wavelength of light was by Thomas Young in 1802.
Note: John William Strutt, 3rd Baron Rayleigh, of “Rayleigh Criterion” fame was born in 1842.