During a debate Flatzoid claimed that celestial navigation uses triangulation. When asked for citations, as he went through citations, he refused to go in to the citations and show how triangulation was used. He would only read the abstract or introduction. After multiple requests he did go into a citation, it was clear he never read the contents as it didn’t show triangulation being used in celestial navigation.
Flatzoid did send the complete list later, so I appreciate that. This is a review of these citations and a search for where triangulation is used in the process of celestial navigation. Starting with the citation that he did bring up.
Institute of Navigation: Navigational Lesson 4: Getting it Right

tl;dr: Nowhere does this show triangulation in celestial navigation.
This is a lesson for 7th graders. It covers calculation, approximation, geometry, trigonometry. There is no part of lesson 4 that covers how to perform celestial navigation. There is an introductory section on the basics of how a sextant measures angles. Followed by a trigonometry review. This review covers triangulation but does not apply trigonometry to celestial navigation, it’s just a review like any geometry textbook would have.
There is a section on triangulating the distance to a rocket ship on its way to the moon 382,700km away. First Law of Flerf confirmed.
Flatzoid referenced page 29 where is lists the formula for Dip Correction. DIP = 1.753 * sqrt(H). When asked where 1.753 came from he had no idea. This is the formula for dip on the surface of the globe using the measured radius of the globe, including refraction. Here is the formula, thanks to Walter Bislin:

First Law of Flerf confirmed again.
Looking at other lessons in this same series there is triangulation for navigation using landmarks, not measuring angles to stars. Reviewing the entire lesson, there is no treatment of celestial navigation at all. But there is coverage of using Global Positioning System. First Law of Flerf confirmed again.

Heavenly Mathematics: The Forgotten Art of Spherical Trigonometry by Glen Van Brummelen, Chapter 9
Clearly Flatzoid didn’t read the title. He didn’t read any of the book. The link is just to the abstract for Chapter 9, which he certainly didn’t read. Since he only looked at the abstract, I’ll quote it here:
This chapter explains how the star is used to find one’s position on the Earth while in a ship at sea. Trigonometry was first used for navigation by fourteenth-century Venetian merchant ships. Several navigational techniques can be identified from navigators’ personal notebooks, including the table of marteloio. Essentially an application of plane trigonometry, marteloio was part of a group of methods known today as “dead” reckoning. Between 1730 and 1759, a clockmaker by the name of John Harrison constructed a series of four chronometers that could keep remarkably accurate time, even on a ship tossed by waves. The chapter considers the use of the method of Saint Hilaire (also called intercept, cosine-haversine, or Davis’s method) to determine three quantities of a star in an astronomical triangle: latitude, declination, and local hour angle. It also discusses the use of the Law of Cosines to solve the star’s altitude.
Flatzoid claims that triangulation is used for celestial navigation. This abstract does mention trigonometry, which, in Flatzoid’s mind, can only mean one thing celestial navigation triangulation. If he had read just the first page he would have seen this:

But Flatzoid didn’t read his own citation. So much for flat earthers “doing their own research”. Unfortunately for Flatzoid, I did his research for him and read the entire chapter. There is a section on triangles. But, it’s just another instance of the First Law of Flerf because the triangle is a spherical triangle.

Not only is this a spherical triangle, something totally anathema to the idea of the flat earth dirt pizza, but it’s also not triangulation. Instead it is a technique to determine the observer’s position on the surface of a sphere. This includes an application of the Haversine formula, which is a difficult method if you lack a modern calculator. The chapter covers solving the spherical triangle using The Method of Saint Hilaire.
This citation completely and totally contradicts doing celestial navigation using flat earth, never showing anything remotely related to doing triangulation with celestial navigation. This diagram makes it clear that the actual method uses the globe:
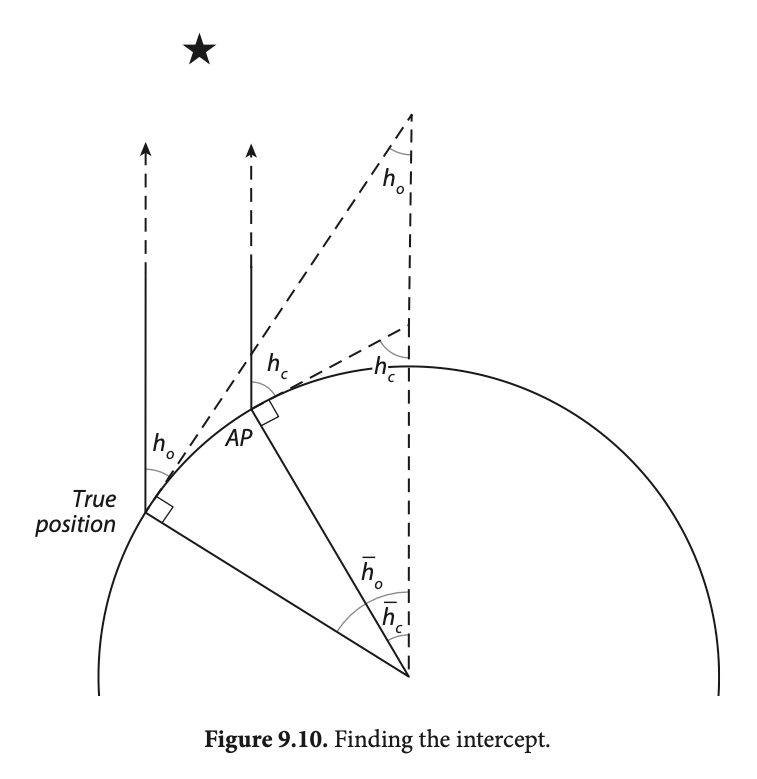
The Mathematical Dynamics of Celestial Navigation and Astronavigation by Kenneth William Spinka
https://teachersinstitute.yale.edu/curriculum/units/2007/3/07.03.09.x.html
Flatzoid references only the first paragraph of the introduction where he finds the word “Trigonometry”.

Flatzoid does not know how to solve a triangle. He couldn’t even do it if he was allowed to google “online triangle calculator”. But, he has a vague idea that trigonometry is involved. He does like to say “SOH CAH TOA”, the mnemonic to remember the trig functions when solving a right triangle. But, he could never use them to solve a triangle.
To Flatzoid using Trigonometry is equal to “triangulation”. This is incorrect, yet somehow he further makes the leap to thinking it means “triangulation to do celestial navigation”.
If Flatzoid had read the citation he would discover that “triangulation” is never mentioned. WHen trigonometry is mentioned, it confirms the First Law of Flerf yet again:


Once again, at no point in the entire citation is triangulation used for celestial navigation.
Trigonometry in Navigation: Unravelling the Secrets of Finding Your Way! by Ms. Anjali, Assistant Professor, Department of Mathematics, Lingaya’s Vidyapeeth Deemed university
This is simply an overview of a blog. It is the first entry and has no coverage of the topics in detail. It says nothing about triangulation. Once again, Flatzoid appears to have equated “trigonometry” with “celestial navigation using triangulation”. Using “trigonometric principals” does not imply what he desperately wants it to mean.

REAL LIFE APPLICATIONS OF TRIGONOMETRY by Mathnasium
https://www.mathnasium.com/blog/real-life-applications-of-trigonometry
Again, nothing showing triangulation in celestial navigation. Simply a passing reference to trigonometry used in the broader field of navigation.

Geometry for Navigation by Erik Engheim
https://erik-engheim.medium.com/geometry-for-navigation-c975c41bdcaa
This article on Medium requires a paid subscription to view it. There are other methods which I won’t detail. It is obvious again that Flatzoid didn’t employ these methods, nor did he pay for a subscription. The only thing he read was the title:

For a change the word “triangulation” is actually present. But, does it support his claim? Does the article show the process for obtaining a position fix using triangulation on flat earth?
No.
It talks about some principals of trigonometry and triangulation. The article gives an rough overview of using trilateration on the globe to get one’s position fix. First Law of Flerf confirmed again.

Thesaurus entry for Celestial Navigation and Triangulation
https://thesaurus.plus/related/celestial_navigation/triangulation
No process for performing celestial navigation using triangulation is to be found here. Just a thesaurus entry showing that the concepts are related.
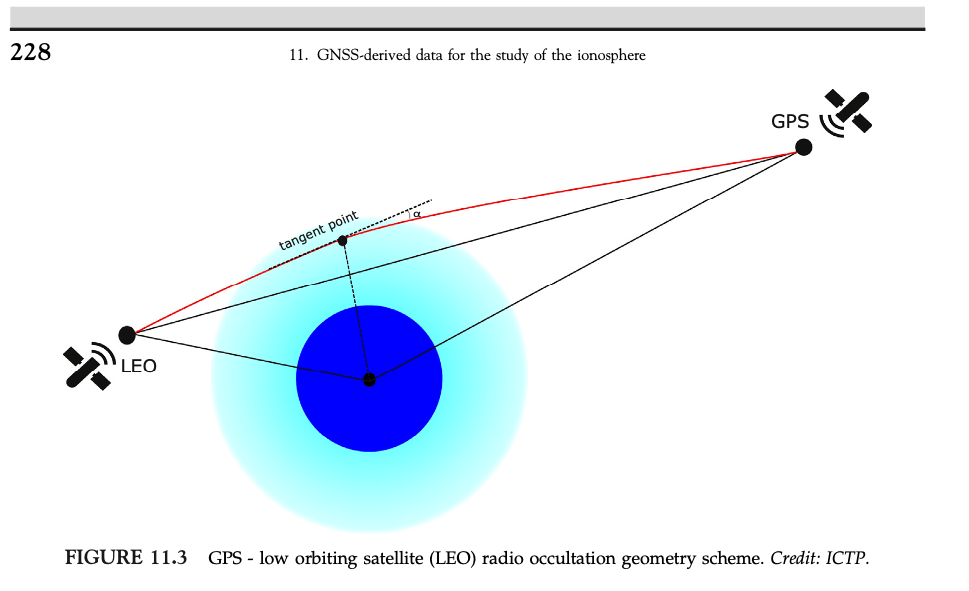
GPS AND GNSS TECHNOLOGY IN GEOSCIENCES edited by George p. Petropoulos and Prashant K. Srivastava
This is the result of a Google cherry picking expedition. The page is an overview of the book. The book is 440 pages long and can be found online in PDF form using methods I won’t detail here.
This book covers how the Global Positioning System (GPS) and Global Navigation Satellite System (GNSS) are used in the Geosciences. The cherry picked section is from Chapter 1, Introduction to GPS/GNSS technology.
In the book the terms “triangulation” and “trilateration” are used interchangeably.

When the details of the process are described, it never uses triangulation, only trilateration.
Using satellites.
Orbiting the globe.
How many times can Flatzoid confirm the First Law of Flerf?